\( \newcommand{\sech}{\operatorname{sech}} \) \( \newcommand{\inverse}[1]{#1^\leftarrow} \) \( \newcommand{\<}{\langle} \) \( \newcommand{\>}{\rangle} \) \( \newcommand{\vect}{\mathbf} \) \( \newcommand{\veci}{\mathbf{\hat ı}} \) \( \newcommand{\vecj}{\mathbf{\hat ȷ}} \) \( \newcommand{\veck}{\mathbf{\hat k}} \) \( \newcommand{\curl}{\operatorname{curl}\,} \) \( \newcommand{\dv}{\operatorname{div}\,} \) \( \newcommand{\detThree}[9]{ \operatorname{det}\left( \begin{array}{c c c} #1 & #2 & #3 \\ #4 & #5 & #6 \\ #7 & #8 & #9 \end{array} \right) } \) \( \newcommand{\detTwo}[4]{ \operatorname{det}\left( \begin{array}{c c} #1 & #2 \\ #3 & #4 \end{array} \right) } \)

Section 4.3 Calculus 2

Polar Coordinates
  1. Home
  2. Resources
  3. Calculus 2
  4. Section 4.3 Calculus 2

4.3 Polar Coordinates

4.3.1 Definition of Polar Coordinates

  • The polar coordinate \(p(r,\theta)\) is defined to be Cartesian coordinate \((r\cos\theta,r\sin\theta)\).
  • Example Plot the polar coordinates \(p(2,\pi/3),p(\sqrt{2},3\pi/4),p(-2,4\pi/3),p(4,11\pi/6)\).
  • Note that every polar coordinate \(p(r,\theta)\) is equal to \(p(r,\theta+k\pi)\) for all even integers \(k\), and equal to \(p(-r,\theta+k\pi)\) for all odd integers \(k\).

4.3.2 Equations Relating Polar and Cartesian Coordinates

  • Polar and Cartesian coordinates may be related by the equations \(x=r\cos\theta\), \(y=r\sin\theta\), \(x^2+y^2=r^2\), and \(\tan\theta=\frac{y}{x}\).
  • Example Convert the Cartesian coordinate \((-2\sqrt3,2)\) into a polar coordinate.
  • Example Convert the polar equation \(r=\frac{1}{\sin\theta-\cos\theta}\), \(\pi/4<\theta<5\pi/4\) into a Cartesian equation.
  • Example Convert the Cartesian equation \((x-2)^2+y^2=4\) into a polar equation.

4.3.3 Common Polar Equations

  • The equation \(r=R\) is a circle centered at the origin of radius \(R\).
  • The equation \(r=D\cos\theta\) is the circle with diameter \(D\) tangent to the \(y\)-axis at the origin.
  • The equation \(r=D\sin\theta\) is the circle with diameter \(D\) tangent to the \(x\)-axis at the origin.
  • The equation \(\theta=\alpha\) is the line passing through the origin at the angle \(\alpha\).
  • The equation \(r\cos\theta=a\) is the vertical line \(x=a\).
  • The equation \(r\sin\theta=a\) is the horizontal line \(y=a\).
  • Example Sketch the region where \(0<\csc\theta\leq r\leq 2\).
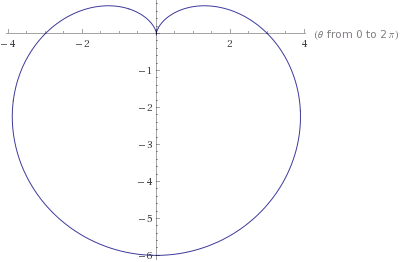
  • The equations \(r=a\pm a\cos\theta\) and \(r=a\pm a\sin\theta\) are known as cardioids.
  • Example Sketch the cardioid \(r=4-4\sin\theta\).

Review Exercises

  1. Convert the polar coordinates \(p(\sqrt 3,2\pi/3),p(\sqrt 2,\pi/4),p(2,7\pi/6),p(-\sqrt 3,-\pi/3)\) to Cartesian and plot them in the \(xy\) plane.
  2. Convert the Cartesian coordinates \((4,-4),(-\frac{3}{2},-\frac{\sqrt 3}{2})\) into polar coordinates.
  3. Convert the polar equation \(r=\frac{5}{\sqrt{25-9\sin^2\theta}}\) into a Cartesian equation. Name the curve.
  4. Convert the Cartesian equation \(1-\frac{y}{x^2+y^2}=\frac{3}{\sqrt{x^2+y^2}}\) into a polar equation.
  5. Convert the Cartesian equation for the line \(y=\frac{x}{\sqrt 3}\) into a polar equation.
  6. Sketch the region where \(0< 3\sec\theta\leq r\leq 6\cos\theta\). (Hint: Completing the square in \(x^2-6x+y^2=0\) yields \((x-3)^2+y^2=9\).)
  7. Sketch the cardioid \(r=3+3\sin\theta\).
  8. Sketch the cardioids \(r=1+\cos\theta\) and \(r=1-\cos\theta\). At what points do they intersect?
  9. Sketch the “three-leaved rose” \(r=\sin 3\theta\).
  10. What polar coordinate gives the Cartesian coordinate \((-\sqrt3,1)\)?
  11. Convert the circle \(x^2+(y-4)^2=16\) into a polar equation.
  12. What equation gives the curve drawn below?

Cardioid

Solutions 1-5

Solutions 6-12

Textbook References

  • University Calculus: Early Transcendentals (3rd Ed)
    • 10.3